分类简介

分类学习

在分类学习任务中，我们有一组数据点，其中每个数据点都标有一个类别。当前的问题是构建一个模型来预测每个输入数据点的正确类别。

分类问题的最简单版本是二元分类问题。在这个问题中，我们只有两类数据点可以被标记。在下面的例子中，我将处理一个二元分类问题，其中一些数据点被标记为类别0，而其他数据点被标记为类别1。我们的目标是构建一个模型，该模型将输入一个数据点并输出0或1来预测该数据点的分类。

下图显示了一个非常简单的二元分类问题。数据集中的每个数据点都由单个变量x描述，这使得可以在一条线上绘制点。然后用颜色表示这些点的分类。黑点为0类点，红点为1类点。

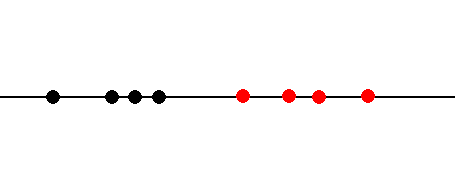决策函数

将这些点划分为不同类别的一个粗略而简单的方法是引入一个决策函数：

D (x,b) = x - b

决策函数依赖于参数b，它是函数与轴相交的点。

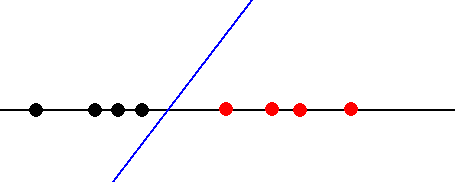我们将决策函数与分类函数结合使用

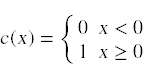
预测输入数据点xi的分类：

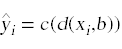
这个过程将赢博体育决策函数为正的点分类为1类点，将赢博体育决策函数为负的点分类为0类点。如果我们正确地选择了模型参数b，模型将正确地区分赢博体育的点。

我们说参数b决定了模型的决策边界。

误差测量和学习

在更复杂的问题中，我们无法事先知道如何设置模型参数来产生正确的分类行为。在这些情况下，我们将遵循调整模型参数的策略：

从模型参数的随机值开始。
估计模型误差。
使用误差估计来调整模型参数，直到不再有任何误差。

下图显示了如果我们最初在模型中设置了错误的模型参数，我们将面临的情况。

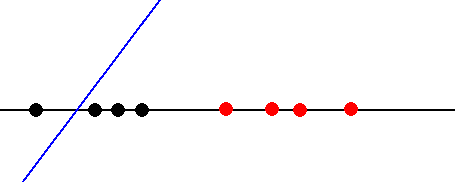在这种情况下，决策函数会错误地将一些0类点分类为1类点。为了测量分类误差，我们可以构造一个合适的误差函数：

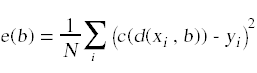
这个特定的误差函数测量了分类函数对数据集中赢博体育点求和的均方误差。yi值给出了数据集中每个点的正确分类。对于我们正在使用的分类函数，这个误差函数测量分类器分类错误的数据点的比例。

我们的目标是调整b使误差减小到0。一种方法是使用误差函数对b求导迭代学习算法

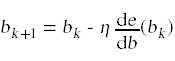
利用误差测量的导数来计算新的模型参数。学习算法利用学习率项η来控制我们调整模型参数的速率。在典型的赢博体育中，几轮学习足以调整模型参数以将误差项减小到0。

逻辑回归

我上面概述的方案的唯一问题是，我构造的误差函数实际上是不可微的。原因是我们在分类器中使用的分类函数c(x)是不可微的。

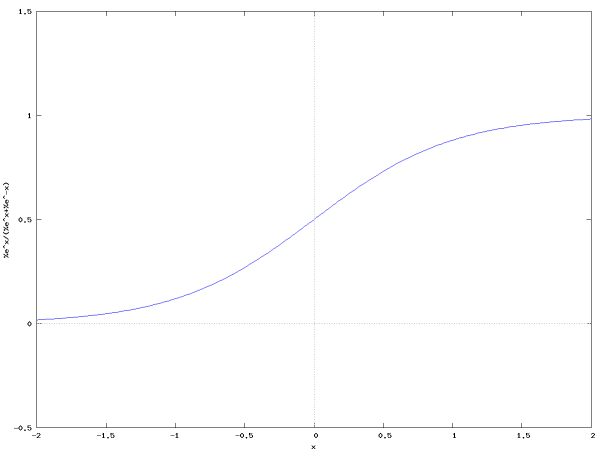
解决这个问题的方法是用光滑的可微函数代替我们的分类函数。为此，最广泛使用的选择是逻辑函数

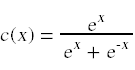
这是这个函数的曲线图。

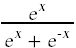注意，这个分类函数的设计目的是输出0到1范围内的分类。您可以将此分类函数的输出视为分类器对某一特定点属于类别1的置信度的度量。

如果我们使用这个逻辑分类函数来计算分类c(d(x,b))，我们说我们已经构建了一个逻辑回归模型。

由于逻辑分类函数对模型参数b是可微的，我们现在可以使用我们的学习算法

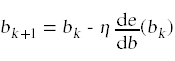
迭代地调整模型参数，从初始猜测b0，直到我们将误差减少到0。

模糊模型

在一些问题中，我们遇到两组点之间没有明确边界的情况。下面是简单的一维分类问题的一个更具挑战性的版本。

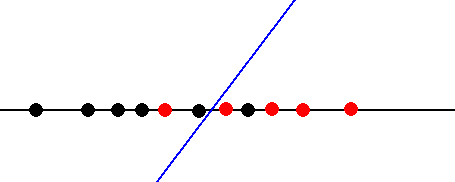这一次的问题是，没有地方放置决策边界来清晰地分离两组点。无论我们把决策函数放在哪里，我们最终都会对至少一些点进行错误的分类。我们所能期望的最好结果是通过学习算法选择一个模型参数b，使误差函数e(b)最小化。这里的区别在于e(b)的最小值不再是0。

在这种情况下，决策函数不可避免地会产生假阳性和假阴性。假阳性是指0类点被错误地归类为1类点。在上图中，蓝线右边的一个黑点是假阳性。假阴性是指1类点被错误地归类为0类点。在上图中，蓝线左边的一个红点是假阴性。

在这种情况下，我们可以引入两种进一步的误差测量，称为精确度和召回率。这些量是根据这四个计数来定义的。

数	解释
TP	真正：有多少1类点被归为15
《外交政策》	误报：有多少0类点被归为0
FN	假阴性：有多少1类分数被归为0
TN	真负：有多少0类分数被归为0

根据这些计数，我们定义

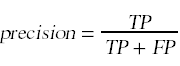
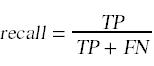
精确度衡量的是我们的模型分类为15的点中有多少是真正的15，而召回率衡量的是我们将真正的15分类为15的那一部分。

阈值

在数据点难以清晰分离的情况下，我们可以将这种情况描述为具有模糊区域。这是决策边界附近的一个区域，决策函数在正确分类数据点方面存在一些困难。下图显示了由一对绿线包围的区域。

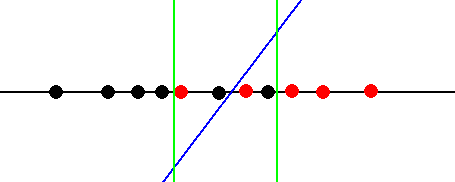在右边绿线的右边，决策函数正确地将赢博体育1类点分类为15。在左边绿线的左边，决策函数正确地将赢博体育类别0点分类为0。

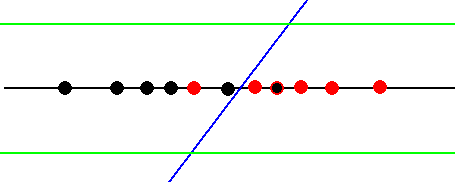
创建这样一个区域的一种方法是使用阈值的概念。我们选择一些数字t，并说决策函数将输入x分类为1，如果d(x) > t。下图显示了t的两种不同选择。如果我们将阈值设置为t的较高值，决策函数将只挑选真正属于类别1的点。如果我们把它设为t的较低值，决策函数就会把确实都是0的东西归为0。

多因素分类

到目前为止，为了使事情保持简单，我只使用了一个具有一个输入因素的示例。我们将为分类任务构建的大多数模型将涉及多个因素。下面的讨论显示了我们如何将处理一个因素的想法推广到具有多个输入因素的问题。为简单起见，我将使用两个输入因子。我所说的关于两个输入因素的一切都可以推广到多个输入因素。

下图显示了双因子空间中的一组数据点。同样，得分分为两类：0类得分为黑色，1类得分为红色。

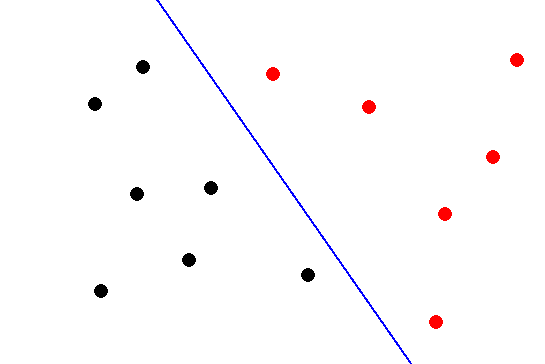该模型的决策函数为

D (x, b) = b0 + b1x1 + b2x2

决策函数的图看起来像一个平面。决策函数在（x1, x2）平面上的直线上等于0，称为决策边界。如果有可能画出一个决策边界，将这两类点清晰地分开，我们就说这些集合是线性可分的。

该模型的误差函数以一种自然的方式进行推广：

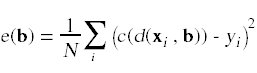
这里唯一的区别是，现在我们的模型中不是只有一个参数，而是有一个参数向量b。为了最小化误差函数，我们使用了一维学习规则的一般化：

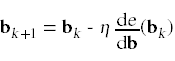
将导数项推广到多个维度，即误差函数的梯度：

Bk +1 = Bk - η∇e（Bk）

该学习规则实现了梯度下降学习算法。