一个问题

这是计算机科学中的一个重要问题。

如果一个算法需要1秒处理N个项目，

处理100n件需要多少时间？

对这个问题最天真的回答是假设算法的运行时间直接与数据集的大小成比例。如果N条处理时间为1秒，则100n条处理时间为100秒。

正如我们将看到的，这种情况几乎从来没有发生过。对于大多数算法，随着要处理的数据集的大小增加，算法的运行时间不会以简单的线性方式增长。

在这些笔记中，我们将开始最新体育赛事资讯、实时赔率分析及在线投注平台探索用于估计常见算法运行时间增长率的技术。

第一个定义

这是我们将在讨论中遇到的第一个定义。

特定算法处理包含N项的数据集所需的时间为T(N)。

不幸的是，这个简单的定义立即引发了许多重要的问题。下面的一些观察结果将使这一定义复杂化。

1. 处理时间可能取决于数据集和算法以外的因素。例如，我们运行算法的CPU的速度和用于编码算法的语言可能会在运行时产生差异。
2. 对于许多算法，可能有许多不同的输入数据集，这些数据集可能会导致算法的运行时间发生变化。

由于这些原因，以及我们在学习过程中会遇到的其他原因，T(N)并不是解决我们核心问题的最有用的方法。同时，回想一下我在讲义开始时问的问题，比起T(N)我们更关心的是随着N的增长T(N)的增长率。

算法分析

到目前为止，我所介绍的问题和思想都是计算机科学中一个重要领域的一部分，即算法分析。解释什么是算法分析的最好方法是从一个具体的例子开始。下面是一个常见排序算法——选择排序的伪代码。

void sort(int A[],int N) {int N = 0；while(n < n) {int smallest = A[n]；Int where = n；Int k = n + 1；while(k < N) {if（A[k] <最小）{最小= A[k]；式中= k；} k = k + 1；} A[where] = A[n]；A[n] =最小；N = N + 1；}}

分析的下一步是用这些语句运行所需时间的信息以及语句执行次数的计数对源代码进行注释。

void sort(int A[],int N) {int N = 0；/ / c1， 1次while(n < n) {//c2 , N+ 1 times int = A[n]；//c3 , N乘以int where = n；//c4 , N乘以int k = n + 1；//c5 , Ntimes while(k < N) {//c6 , 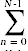 (N - n)乘以if（A[k] <最小）{//c7 ,  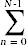(N - n- 1)倍最小= A[k]；//c8, ? ?乘以where = k；//c9, ? ?乘以}k = k + 1；//c10 ,  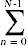(N - n- 1) times} A[where] = A[n]；//c11 , N乘以A[n] =最小；//c12 , N乘以n = n + 1；//c13 , N次数}}

这里一个直接的不确定性是if语句体中的语句被执行的次数。由于if语句中的测试并不总是求值为true，因此这些语句将运行许多次，这是无法确定的。对于这些语句，我们能做的最好的事情就是给它们执行的次数设置一个上限。语句体中语句执行次数的上限是if测试执行的次数。

接下来，我们需要简化上面出现的求和。为此，你需要记住你在微积分中学过的计算和的标准技巧。

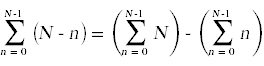
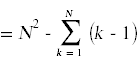
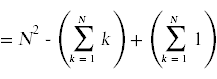
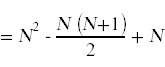
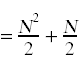
同样的,

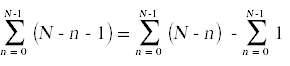
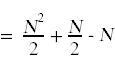
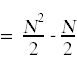
这里也是带注释的源代码，其中简化了求和，并在右侧显示了每个语句的总运行时间，其中考虑了每个语句执行的次数。

void sort(int A[],int N) {int N = 0；/ / c1while(n < n) {//c2 (N+ 1) int = A[n]；//c3 NInt where = n；//c4 NInt k = n + 1；//c5 Nwhile(k < N) {//c6 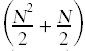如果（A[k] <最小）{//c7 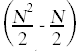最小的= A[k]；/ /≤c8  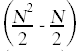式中= k；/ /≤c9 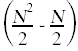} k = k + 1；//c10 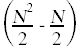} A[where] = A[n]；//c11 NA[n] =最小；//c12 NN = N + 1；//c13 N}}

现在我们可以将算法中赢博体育语句的运行时间加起来。为了强调这个总和对N的依赖，我将重新排列总和中的项：

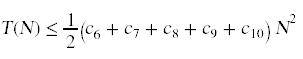
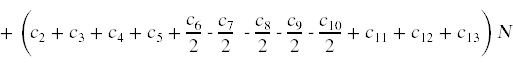
+ （c1 + c2）

因为赢博体育这些常数都是未知的，我们可以把我们的无知整合成一些更简单的系数。

T(n)≤c1 n2 + c2 n + c3

现在我们可以对这个算法的T(N)的增长率说一些具体的东西：随着要排序的列表的大小的增长，运行时间呈二次增长。

大0符号

正如我们在上面的例子中看到的，在大多数情况下，当我们试图估计一个算法的运行时间时，我们最终会为运行时间开发一个上限。这激发了以下重要的定义：

如果存在一个常数C和一个N0 >，使得对于赢博体育n≥N0， f(n)≤C g(n)，则称函数f(n)为O（g(n)）。

这是课本上的一张图片，说明了这个定义中的关键思想。

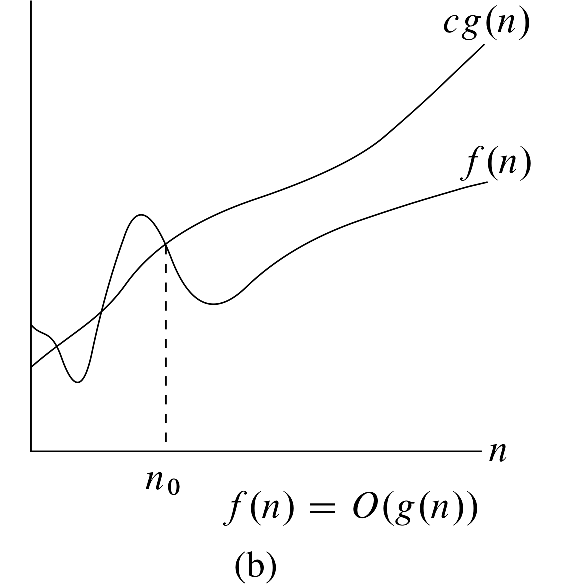
这里的主要思想是我们想用一个简单的函数g(n)来给一个更复杂的函数f(n)的增长设定一个严格的上界。

我们为选择排序计算的T(N)是O（N2）因为

T(n)≤c1 n2 + c2 n + c3≤c n2

选C。

另一个例子

在课本的第二章中，你会发现一个类似的插入排序算法的分析。

下面是一些用于插入排序的带注释的伪代码。

选择排序和插入排序之间一个有趣的区别是两种算法在运行时的不确定性。选择排序中的一个小不确定性是if语句体中的语句被执行多少次。这种不确定性很小，因为即使我们假设if语句体中的语句永远不会运行，我们仍然会得到运行时间的上限O(N2)，因为我们知道if语句中的测试必须执行可预测的次数，无论数据集是什么样子。插入排序包含较大的不确定性。插入排序中的不确定性是在for循环的每次迭代中while循环执行了多少次。

对于插入排序中的while循环，我们所能做的就是为它在外循环的每次迭代中运行的次数设置界限。下限是当我们第一次遇到while循环中的测试时，它立即被求值为false。这导致插入排序在最佳情况下的运行时间估计为O(N)。上限是每次执行外循环时，while循环一直运行，直到i达到0。这将导致最坏情况下插入排序的运行时间估计为O（N2）。

关于插入排序，一个更有用的问题是内循环平均运行多少次。为了回答这个问题，我们需要引入一些概率论的思想。我们将在第5章回到这个问题。