快速排序算法

QUICKSORT（A,p,r）如果p < r q = PARTITION(A,p,r) QUICKSORT(A,p,q-1) QUICKSORT(A,p,q-1) QUICKSORT(A,p,r) PARTITION(A,p,r) x = A[r] i = p-1 for j = p到r-1如果A[j] <= x i = i+1交换A[i]与A[j]交换A[i+1]与A[r]返回i+1

计算快速排序的运行效率

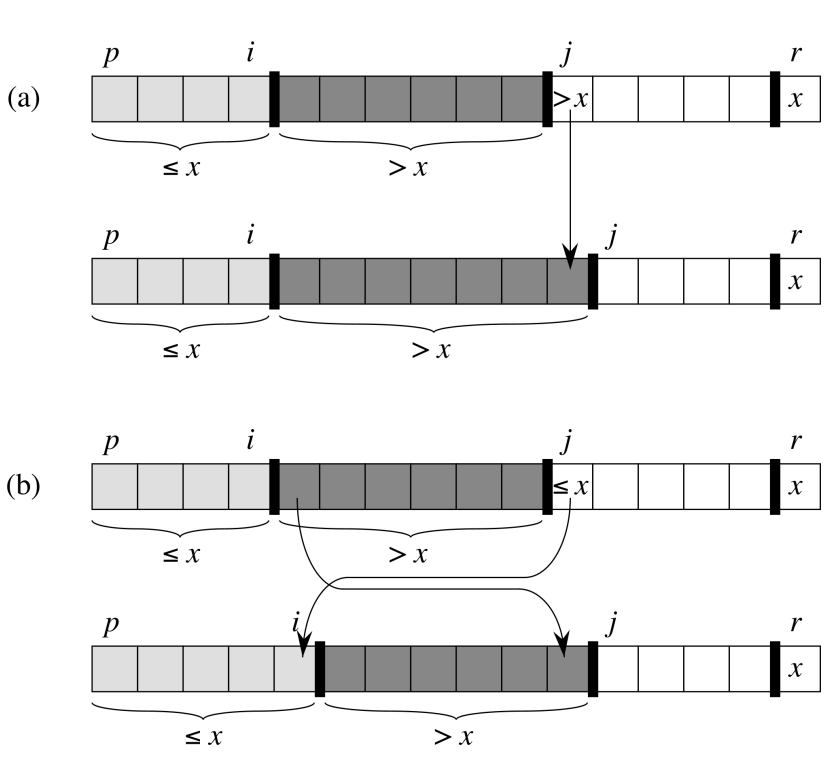
以下是关于快速排序行为的一些关键观察：

1. 快速排序所做的几乎赢博体育工作都发生在对Partition的调用中。
2. 在对Partition的调用中，最常见的操作之一是比较测试。
3. 在对Partition的调用中完成的总工作量以运行比较测试的次数的某个倍数为限。
4. 比较测试将当前枢轴与子数组中的其他数字进行比较。
5. 一旦某个号码成为对Partition调用中的枢轴，其他对Partition的调用将不会以任何方式使用该号码。
6. 如果我们按照排序后在数组中的最终位置对原始列表中的数字进行索引，那么我们可以看到x_我会被拿来和x_j当且仅当这两个数中的一个是主数在它们之间的任何一个数被选为主数之前。

这是一个估计比较总数的概率论证。

引入随机变量

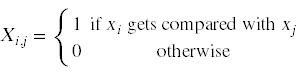
对于这个变量，表示总比较次数的随机变量是

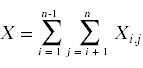
我们想要计算X的期望值，这将产生快速排序中比较的总次数。

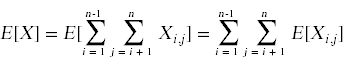
E[Xi，j]就是Xi相对于xj的概率。这个概率是多少？最简单的方法是计算xi不与xj比较的概率：如果xi和xj之间的任何一个数被选为首先的主值，这种情况就会发生。假设每个数字被先选的概率相等，这个概率很简单

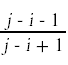
因此

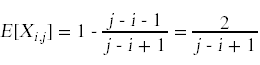
和

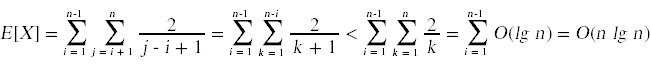
随机快速排序