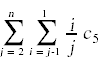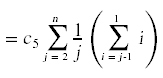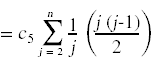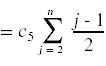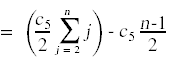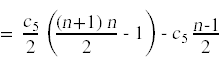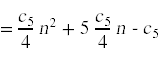随机变量

离散随机变量X是一个变量，它可以取一系列离散值X1， X2，…，Xn，并具有相关的概率p1， p2，…pn。

期望值E{X}由表达式给出

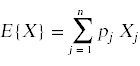
在概率论中，我们也研究事件。假设一个系统可以处于几种不同状态中的一种。当系统陷入与事件相关的特定状态时，就会发生事件A。在概率论中，我们试图计算某些事件发生的概率：假设我们已经确定事件A发生的概率为p。

我们可以将一种特殊的随机变量与事件a联系起来，这种随机变量称为指标随机变量，写为I{a}或XA。如果a出现，指标随机变量的值为1，如果a不出现，则为0。由此，我们可以计算出XA = I{A}的期望值：

E{X_A} = p·1 + (1-p)·0 = p

成本和随机变量

在估计特定算法的运行时成本时，我们有时必须处理不确定事件。也就是说，我们可能会看到一个算法或算法的一部分，它会根据我们正在处理的数据的性质表现出一系列不同的行为（以及相关的成本）。如果我们可以量化结果的范围（及其相关成本），并将概率附加到这些结果上，我们就可以为成本构建一个随机变量。一旦我们构造了一个适当的随机变量来模拟成本，我们就可以使用概率论方法来计算成本的期望值。

话虽如此，通常没有单一的最佳方法来模拟随机变量的成本。下面我将展示一些例子，展示将成本与随机变量关联起来的一系列策略。

招聘问题

在5.1节中，作者提出了雇佣问题。在招聘问题中，你想要雇佣一个私人助理。一家人事机构有一套n个候选人，他们会把候选人一个一个地发给你，让你评估。

这里有一些进一步的细节。

• 候选人都有不同的资格水平：这使得您可以为每个候选人分配一个等级。没有两个候选人的级别相同。
• 任何时候，如果有一个候选人的级别比你现在的助理高，你就解雇你现在的助理，聘请新的候选人。
• 你付一小笔费用c_我每次中介给你送来候选人。
• 你要付出更高的代价c_h炒掉你现在的助理，雇佣更好的人。
• 你雇佣他们发给你的第一个候选人。
• 候选人以随机的排名顺序到达。

我们想要回答的问题是“对n个候选人进行面试和招聘过程的预期成本是多少？”

我们可以用一段伪代码来总结这一切。

如果候选人i比best - best = i更优秀，则招聘候选人i

对于这个例子，我们想要稍微偏离我们通常估计运行时间的方法。在本例中，我们不想估算运行时间，而是估算总成本。我们通过只给代码中的一些语句附加成本来计算总成本。

招聘助理(n)最优= 0为i = 1到n面试候选人i //成本=c我如果候选人i比best更好，best = i雇用候选人i //成本=ch

这里的复杂之处在于，我们的成本之一与概率事件相关：招聘事件不会在循环的每次迭代中发生。

计算招聘事件成本的正确方法是将其与事件关联起来，并构造一个随机变量来对该事件进行建模。我们构建一个事件

Hi ={候选人i被录用了}

和一个相关的指标随机变量：

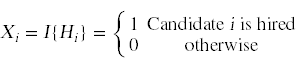
如果我们可以计算出这个随机变量的期望值，我们就可以继续计算总成本：

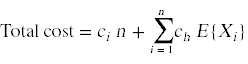
我们可以计算期望一旦我们知道了随机变量Xi的概率分布就可以完成这个计算。这个概率分布取决于一个简单的问题第i个候选人比之前第i-1个候选人更好的概率是多少？如果我们假设问题中的赢博体育i个候选人的排名是随机的，并且候选人以随机的顺序到达，那么任何一个候选人都有相同的概率成为群体中最好的。特别是，最后一个候选人有1/i的概率是最好的。由此我们可以计算

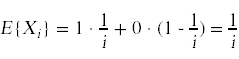
我们现在看到了

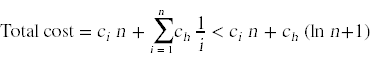
帽子检查问题

这是课本上的一个问题。N个顾客把帽子放在帽子寄存处。当顾客离开时，操作帽子检查的人将帽子按随机顺序归还给顾客。有多少顾客会收到他们自己的帽子？

为了解决这个问题，我们引入了一组指标随机变量

Hi ={顾客i拿回自己的帽子}

一个简单的计数参数表明Hi = 1的概率是

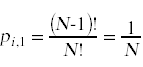
有N个！排列帽子的方法。这些排列（N-1）！在I的位置有一个I。

因此，Hi的期望值为

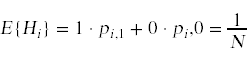
拿回自己帽子的顾客的预期数量是

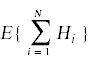
我们想这么说

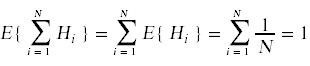
这个证明的问题在于，第一个等式似乎取决于所涉及的随机变量是否独立。这里不是这样，因为Hi变量不是独立的随机变量。例如，如果我告诉你H1等于1，这个信息会影响H2等于2的概率。

然而，事实证明，第一个等式是成立的即使变量不是独立的。让我们考虑一个更简单的等式：

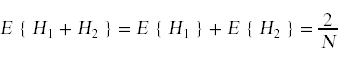
为了证明这个等式，我们考虑组合随机变量H1 + H2的四种可能状态及其相关概率：

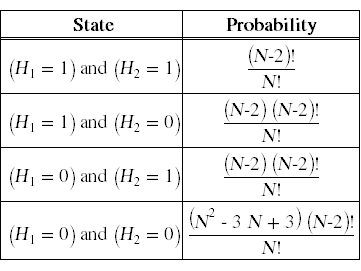
由此我们可以计算出E{H1 + H2}：

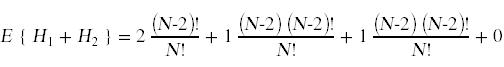
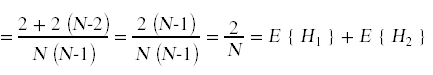
这里所发生的是一个更普遍的原理的例子，叫做期望线性。即使变量Hi不是独立的，它仍然成立

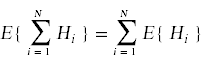
你可以在网上找到很多关于这个原理的证明。这里有一个这样的证明。

插入排序

插入排序是一种稍微复杂的算法，它也需要概率运行时分析。

下面是插入排序的伪代码。

对于j = 2到n key = A[j] i = j - 1而i > 0和A[i] > key A[i+1] = A[i] i = i - 1 A[i+1] = key

这里需要注意的一个关键问题是，最内层循环中的语句是概率语句。根据数据的排列，这些语句可能执行，也可能不执行。正如我们已经看到的，处理概率语句的适当方法是构造一个表示语句执行的事件，然后准备一个相应的指示符随机变量。在本例中，我们想要处理的事件是

Xj,i ={当i和j具有给定值时，语句运行}

这个事件的问题是很难计算出事件的概率。在赢博体育概率论中，我们经常通过将有问题的事件替换为概率易于计算的等效事件来解决此类问题。在这种情况下，我们可以通过考虑以下事件来得到我们想要的：

Yj,i = {A[j]属于位置i或以下}

这个事件发生的概率很容易确定。如果我们假设这些数字是真正随机分布的，那么A[j]在1和j之间的j个可能位置中的任意一个位置的概率为1/j。由此我们可以得出A[j]在i或以下位置的概率为i/j。最后，很容易看出，当且仅当事件Yj，i发生时，内循环中的语句才会运行。

有了这些基础，我们现在就可以计算插入排序的代价了。这是附带费用的代码。在语句是概率性的情况下，成本表示为成本与随机变量{该语句执行}的组合。

对于j = 2到n // c1
  key = A[j]                 //  c2I = j - 1 // c3而A[i] >键// 
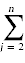
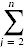
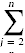
    A[i+1] = A[i]            //  Yj，我 c5I = I - 1 // Yj，我 c6
  A[i+1] = key               //  c7

最后一步是计算赢博体育这些成本的期望值。对于非概率的成本，成本就是指示的总和。例如,

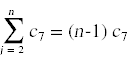
为了计算随机变量存在的期望，我们做以下操作：

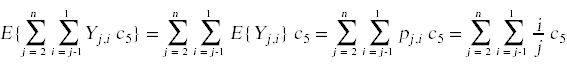
现在我们已经把事情简化到可以计算总和的地步了：