通过递归计算组合
的结合象征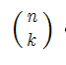 
或“n选择k在数学中有很多赢博体育。概率论中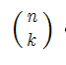计算有多少种方法可以得到k序列中的正面n投掷一枚均匀的硬币。
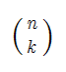是通过公式计算的吗
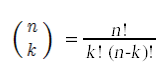
有两种特殊情况很容易计算。
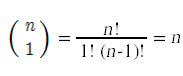
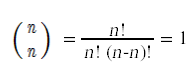
计算组合的一种方法是计算赢博体育涉及的阶乘，然后将分母除以分子。这对于大于8的n是不实用的，因为n！将不适合32位整数，即使最终结果可以。相反，计算组合最常见的方法是利用这种递归关系：
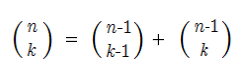
这种递归关系加上这两种特殊情况使得在C中构造递归函数定义来计算组合成为可能。
int C(int n,int k) {if（k == 1）返回n；如果（k == n）返回1；返回(n, k - 1) + C (n, k);｝
这是可行的，并且确实计算出n远远大于8的组合的正确值。
这种方法确实有一个缺陷。考虑一下当我们尝试计算C（8,5）时会发生什么。
C（8,5）呼叫C（7,4）和C(7,5) C（7,4）呼叫C（6,3）和C(6,4) C（7,4）呼叫C(6,5) C（7,5）呼叫C(6,5) C（7,5）呼叫C(6,4) C（6,3）呼叫C（5,2）和C(5,3) C（6,4）呼叫C（5,3）和C(5,4) C（6,4）呼叫C（5,3）和C(5,4) C（6,5）呼叫C（5,4）和C（5,5）
过了一段时间，你开始注意到同一个函数被多次调用。对于较大的n和k，这种影响变得非常严重，以至于上面显示的简单递归函数变得非常低效。
我们可以构建一个程序来说明这个问题有多严重。诀窍是声明一个全局二维数组
int数[101][101];
它存储的信息是，对于每一对参数值n和k，我们调用C的次数。
在程序开始时，调用该函数将赢博体育计数设置为0：
无效initCounts(int maxN,int maxK) {int n,k；(n = 1; n < = maxN; n + +) (k = 1; k < = maxK; k + +)计数[n] [k] = 0;｝
然后，我们修改计算组合的函数，以记录每对参数调用它的次数。
int C(int n,int k) {counts[n][k]++；如果（k == 1）返回n；如果（k == n）返回1；返回(n, k - 1) + C (n, k);｝
在程序的最后，我们将这个计数数据转储到一个文件中。
无效saveCounts(int maxN,int maxK) {ofstream out；整数n, k;out.open(“counts.txt”);为(n = 1; n < = maxN; n + +) {(k = 1; k < = maxK; k + +) < < std::环境运输及工务局局长(5)< <计数[n] [k];Out << std::endl；} out.close ();｝
结果令人震惊。下面是我们尝试计算C（16,10）时得到的计数集：
0 0 0 0 0 0 0 0 0 0 1287 1287 0 0 0 0 0 0 0 0 495 1287 792 0 0 0 0 0 0 0 165 495 792 462 0 0 0 0 0 0 45 165 330 462 252 0 0 0 0 0 9 45 120 210 252 126 0 0 0 0 1 9 36 84 126 126 56 0 0 0 0 1 8 28 56 70 56 21 0 0 0 0 1 7 21 35 35 21 6 0 0 0 0 1 6 15 20 15 6 1 0 0 0 0 1 5 10 10 5 1 0 0 0 0 0 1 4 6 4 1 0 0 0 0 0 0 1 3 3 1 0 0 0 0 0 0 0 1 2 1 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 1)
从这个表中我们可以看出，在计算C（16,10）的过程中，C（2,1）、C（2,2）和C（3,2）各被调用了1287次。随着n和k的增大，冗余函数调用的问题会呈指数级恶化。当n = 30时，这种简单的递归计算C（n,k）的方法就完全不实用了。
记忆的结果
消除对递归函数的冗余调用所需的简单修复称为记忆化。其思想是记住我们计算的任何值，以便下次我们被要求计算一个值时，我们可以查找它，而不是重新计算它。这对于具有中等数量整数参数的递归函数最有效。在这种情况下，我们可以通过将值存储在表中来记住前面计算的值。每当要求我们计算一个值时，我们首先查阅表。
对于计算组合的函数，我们进行如下操作。我们首先创建一个全局二维数组来保存记住的函数值。
#define MAX_N 40 #define MAX_K 40 int c[MAX_N+1][MAX_K+1]；
在程序开始时，在我们尝试计算任何组合之前，我们将表中的赢博体育值初始化为一个标记值，该值表示尚未计算任何值。对于这个赢博体育程序，0可以作为一个合理的标记值。
void initTable() {int n,k；(n = 0; n < = MAX_N; n + +) (k = 0; k < = MAX_K; k + +) c [n] [k] = 0;｝
然后重写递归函数以使用该表。每当我们被要求计算特定n和k的C（n,k）时，我们首先检查表，看看是否已经计算过了。如果还没有计算，则在返回结果之前计算它并将值保存在表中。
int C(int n,int k) {int result = C [n][k]；如果（结果== 0）{如果（k == 1）结果= n；否则if(k == n) result = 1；= C(n-1,k-1)+C(n-1,k)；C [n][k] =结果；}返回结果；｝
动态规划
记忆解的一个有趣的副作用是，它最终用c （n,k）的值填满了表c[n][k]。
有效解决组合问题的更直接方法是编写代码，用正确的值填充表。这就是所谓的动态规划策略。
我们可以用一个函数来做
void initTable(){//为c[n][k]填充正确的值//对于赢博体育n和k的值}
一旦c数组正确地填满了值，我们就可以重写函数来计算组合
int C(int n,int k) {if(k <= n) return C [n][k]；否则返回0；｝
要编写initTable函数，我们只需要复制原始递归解决方案中的逻辑
int C(int n,int k) {if（k == 1）返回n；如果（k == n）返回1；返回(n, k - 1) + C (n, k);｝
在一组循环中。我们需要做两件事。第一种方法是写一对循环来填充基本情况中赢博体育n和k的c[n][k]项。组合的基本情况是k = 1和k = n：
void initTable() {int n, k；//为（n = 0;n <= MAX_N;n++） {c[n][k] = 1；C [n][1] = n；C [n][0] = 1；}}
最后，我们构建一个循环，为赢博体育剩余的条目填充c[n][k]。在构造循环时，我们必须小心确保c[n][k]的公式只使用循环中已经填入的项。下面是正确的循环结构。
void initTable() {int n, k；//为（n = 1;n <= MAX_N;n++） {c[n][n] = 1；C [n][1] = n；C [n][0] = 1；} / /填写剩余的条目(n = 2; n < = MAX_N; n + +)为(k = 2; k < {n, k + +) c [n] [k] = c (n - 1) (k - 1) + c [n - 1] [k];c[n][k] = 0; （k = n+1;k <= MAX_K;k++）}}