RSA的数学和算法背景
欧几里德算法
两个正整数a和b的最大公约数gcd（a,b）是能被a和b整除的最大整数。计算gcd的算法基于gcd的两个性质。如果a是两个数中较大的一个
Gcd (a,b) = gdc（a mod b,b）
Gcd (a,0) = a
从定义来看，第二个性质是显而易见的。你可以在课本中找到定理31.9中第一个性质的证明。这两个性质导致了一种计算两个正整数的gcd的算法，称为欧几里得算法。
欧几里德(一个，b）如果b= = 0返回一个 其他回报欧几里德(b，一个 国防部 b）
下面的结果对于理解其工作原理非常重要，并且本身也很有用。如果d = gcd（a,b）存在整数x和y满足
A x + b y = d
你可以在课本中定理31.2的证明中找到这个事实的证明。这个等式是有用的，原因如下。假设我们从
A x + b y
并寻求一个简单的数学变换，改变其中一些变量的值，同时保持表达式的整体值不变。这种变换的一个简单例子是在ax和byy上加减一个因子bx：
A x + b y = (A x - b x) + (b y + b x) = (A - b) x + b （y + x）
更一般地说，如果k表示b能被a整除的次数我们也可以这样做
A x + b y = (A x - k b x) + （b y + k b x）
= (a - k b) x + b(y + k x) = (a mod b) x + b（y + k x）
最后，如果我们把第二个因子和第一个因子交换位置，我们就有了一个形式的表达式
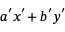
在一个
大于b
赢博体育因子都是整数。总而言之，我们有
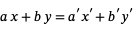
和
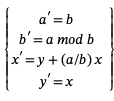
如果我们重复这个过程，最终我们会一个
= d和b
= 0，由一系列等式推导出
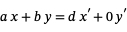
至此，我们看到了最终的x
Value必须是1和finaly
价值可以是任何东西。为了方便，我们可以设置y
= 0。现在我们知道了最终结果x
和y
值是我们可以通过算法的步骤反向工作来恢复原始值x和y值。
 |
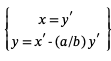（1) |
这里有一个例子。我们从计算147和75的gcd开始。在第一轮中，我们只计算算法中a和b的情况。
| 一个 | b | （一个/b） |
|---|---|---|
| 147 | 75 | 1 |
| 75 | 72 | 1 |
| 72 | 3 | 24 |
| 3 | 0 | - |
在下一关中，我们使用公式(1)从底部向上工作。
| 一个 | b | （一个/b） | x | y |
|---|---|---|---|---|
| 147 | 75 | 1 | 1 | 2 |
| 75 | 72 | 1 | 1 | 1 |
| 72 | 3 | 24 | 0 | 1 |
| 3 | 0 | - | 1 | 0 |
很容易验证这些是正确的x和y值。
A x + b y = 147(-1) + 75(2) = -147 + 150 = 3 = gcd（A,b）
赢博体育这些实际上都很容易通过利用一个特殊的递归技巧来实现。
Extended-Euclid (一个，b）如果b= = 0返回（一个1 0) (d，x
，y
) =扩展欧几里得(b，一个 国防部 b） （d，x，y) = (d
，y
，x
-（一个/b）y
）返回 (d，x，y）
这个算法也是相当高效的。对于给定的一对数字a和b，递归调用的次数是O（lgb）
刻画
我们说两个整数a和b对n取余如果有一个整数y满足
A + n y = b
用来表示同余的符号是
A≡b （mod n）
扩展欧几里得算法对于求解这种形式的同余方程是有用的
ax≡g （mod b）
因为解这个同余等于解
| 一个 x + b y = g | （2） |
当且仅当a和b的gcd均被g整除时，这个方程有解。如果是这种情况，我们可以先用扩展欧几里得算法求解(2)
A x + b y = gcd（A,b）
然后在解的两边乘以g/gcd（a,b）
这里有一些关于同余的有用事实，我们将需要它们来实现RSA算法。第一个叫做小费马定理。如果p是质数a是任意正整数，那么
Ap-1≡1 （mod p）
第二个定理是中国剩余定理的推论。如果p和q是质数
X≡y （mod p）
X≡y （mod q）
然后
X≡y（模p q）
RSA算法
我们现在有了赢博体育的数学机制来开发实现RSA算法所需的数学。
该算法从选择两个大素数p和q开始。从p和q开始构造
N = p q
φ(n) = (p - 1)（q - 1）
下一步是选择一个小的奇数e，使gcd(e,φ(n)) = 1。接下来，我们使用扩展欧几里得算法来计算d，使得
D e≡1 （mod φ(n)）
这相当于说
D e - k φ(n) = 1
对于某个正k或者
D e = 1 + k (p - 1)（q - 1）
如果我们取任意整数M
Md e = M1 + k(p-1)(q-1) = M Mk(p-1)（q-1）
利用小费马定理
Mp-1≡1 （mod p）
如此......以至于......
Md e≡M (Mp-1) k (q1)≡M (1) k (q - 1)≡M p (mod)
和类似的
mde≡M (Mq-1)k(p-1)≡M (1)k (p-1)≡M （mod q）
中国剩余定理的推论现在告诉我们
Md e≡M （mod n）
下面是将消息从a安全地发送到B所需的实际RSA算法中的步骤。
- B选择两个大质数p和q，计算n = p q和φ(n) = (p-1)（q-1）
- B选择一个小的奇数e，使得gcd(e,φ(n)) = 1。
- B使用扩展欧几里德来计算d，使得de≡1 （mod φ(n)）。
- B将（e,n）对作为公钥发布。
- A将他们的消息分解成块，并将每个块转换成一个大整数M。
- A计算出Me （mod n）并将其发送给B。
- B使用（d,n）对作为私钥计算（Me）d≡M (mod n)，从而恢复原始消息M。
其他算法成分
作为最后的实际考虑，我们需要简要讨论一些其他有用的算法，这些算法需要有效地实现RSA算法的某些部分。
我们需要的第一个额外的东西是一个有效的求幂算法来计算像Me （mod n）这样的东西我们实际上在课程开始的时候在循环不变量的讲义中看到过这样的算法。下面是该算法的代码：
Z = x；S = x；T = y - 1；if(t % 2 == 0) {t = t / 2；S = S * S；} else {z = z * s；T = T -1；｝
该算法通过保持不变的xy = z * .来计算xy，这不仅是一个非常有效的算法，而且将其修改为一个对n进行赢博体育算术运算的算法也很简单：
Z = x；S = x；T = y - 1；if(t % 2 == 0) {t = t / 2；S = (S * S) % n；} else {z = (z * s) % n；T = T -1；｝
如果您需要从这个算法中获得更好的性能，您可以使用一种有效的乘法方案（例如FFT乘法）来实现乘法。
有效实现RSA所需的第二个要素是构造大随机素数p和q的方法。所使用的方法基于数论的两个结果。第一个结果表明，在大数中，质数以某种可预测的频率出现。结果是，如果你在一个大数n附近随机选择一个数，那么你随机选择一个素数的几率是1/ lnn。对于RSA的大多数实际赢博体育，人们试图在n = 2124附近找到素数。在那个区域，质数出现的频率很高
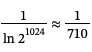
换句话说，如果您生成大约1500个随机的1024位数字，那么其中一个很可能是素数。
我们需要的最后一件事是一些有效的方法来测试候选随机数，看看它们是否是素数。这里，数论又来拯救我们了，它提出了一个叫做伪最优性测试的想法。这个想法是基于小费马定理。如果n是质数，那么
An-1≡1 （mod n）
这个事实的有用之处在于，如果n不是素数，那么对于a的许多选择，an-1通常不等于1 mod n。事实上，如果我们为1024位合数计算2n-1，只有1 / 1041的机会意外地等于1 mod n。我们称2n-1≡1 mod n的数为假素数。伪素数几乎总是素数，只有在极少数情况下才会变成非素数。使用基于这个观察的想法，我们可以快速地从1500个随机候选者中筛选出一个或两个伪素数，然后进行一些更慢、更准确的测试来验证它们实际上是素数。