证明算法是正确的
在第21章和第22章的讲座中,我给出了一些理由,为什么你们应该相信这些算法是正确的。这些原因有助于理解算法是如何工作的,但并不能正式证明算法是正确的。在这些笔记中,我将向你们介绍一个证明框架,它可以用来证明迭代算法是正确的。一旦我们看到了框架在实践中如何使用的几个基本示例,我们将重新审视第21章和第22章中的算法,并给出这些算法的正确性的正式证明。
证明循环是正确的
几乎赢博体育的迭代算法都在一个或多个循环中完成大部分有趣的步骤。在这些笔记中,我将向你们介绍一个证明框架,它可以用来证明一个循环做了我们声称它做的事情。
为了帮助标准化我们的证明框架,我们将使用的赢博体育循环都将具有以下通用形式:
<初始化> while(!<终止>){<主体>}
以下是循环的各个部分将做的事情:
- 的
初始化> <代码将设置循环所需的任何变量。大多数循环都是由循环变量驱动的,所以我们至少需要给循环变量一个初始值。 - 这个循环是由
< >终止条件,它是一个布尔表达式。循环一直运行到< >终止条件为真。 - 这个循环也有一个
身体< >.
并不是我们看到的每个循环都会使用while循环,但是每个循环都可以重写为while循环。
接下来我们要做的是引入一些额外的布尔表达式,称为谓词。这些谓词的目的是帮助表达在循环代码的各个点上我们认为正确的内容。
具体来说,我们将使用三个主要谓词:
- 一个初始化谓词这说明什么是正确的之后
初始化> <在循环开始之前。 - 一个目标谓词,表示在循环结束时什么为真。
- 一个循环不变式在我们运行
身体< >。循环不变式在身体< >运行。
有了这三个谓词,每个证明将由以下步骤组成:
- 在
之后显示初始化谓词为true。 - 说明初始化谓词隐含循环不变量。
- 说明如果循环不变量为真,终止条件为真,那么目标谓词必须为真。
- 显示循环不变式在每次通过循环体后仍然为真。也就是说,如果在运行之前循环不变式为真,那么在运行之后它仍然为真。
例如:快速排序分区
这里再次是快速排序的伪代码:
QUICKSORT(A,p,r)如果p < r q = PARTITION(A,p,r) QUICKSORT(A,p,q-1) QUICKSORT(A,p,q-1) QUICKSORT(A,p,r) PARTITION(A,p,r) x = A[r] i = p-1 for j = p到r-1如果A[j] <= x i = i+1交换A[i]与A[j]交换A[i+1]与A[r]返回i+1
快速排序有两部分,一个递归函数Quicksort (a,p,r)和一个迭代函数partition (a,p,r)。对于第一个例子,我要证明配分函数中的循环符合我们的预期。
第一步是稍微重写代码,使用while循环代替for循环。
分区(A,p,r) x = A[r] i = p-1 j = p while (j < r)如果A[j] <= x i = i+1交换A[i]与A[j] j = j +1交换A[i+1]与A[r]返回i+1
谓词
接下来,我们构造一个合适的目标谓词:
如果这是真的,那么我们就可以安全地将A[i+1]与A[r]交换位置,最终得到配分函数的总体目标:
<分区目标> = (A[p..](A[i+1] = x)和(A[i+2] ..)[R] [R]
循环的终止条件本质上是
<终止> = (j = r)
另一个很容易写下来的谓词是初始化谓词:
最后,我们需要一个循环不变量。这是整个过程中最不明显的部分,需要一些经验才能做好。对于这个例子,我将简单地说明什么是循环不变量,然后我们将继续证明它在证明中是有效的。循环不变量通常是目标谓词的弱化版本。下面是我将使用的循环不变量:
正确性证明
现在我们可以构造证明了。以下是相关步骤:
1)
((p . .p-1] <= x)和(A[p..][P-1] [x]
这将导致一个平凡的真谓词,因为这里提到的两个范围都是空的。
2)
((p . .i] <= x)和(A[i+1..](j=r) => (A[p., p.]i] <= x)和(A[i+1..][1] [x]
3) 之后
((p . .i] <= x)和(A[i+1..]j [1] [j]
复杂之处在于代码可能潜在地改变i和j的值。对于i和j的旧值,不变量可能为真,但在更新这些变量后,它可能不再为真。
让我们从关注身体中经常发生的一件事开始:
J = J + 1
这里的危险在于,如果A[j] <= x,那么增加j将导致(A[i+1..][J-1] > x)不再为真。
解决这个问题的方法是在代码体中添加逻辑来预测并解决这个问题。这就是这部分逻辑背后的动机:
如果A[j] <= x i = i + 1,将A[i]与A[j]交换
这里的解决方法是注意坏情况,然后通过将A[i+1]和A[j]交换位置来修复它。这样做是安全的,因为A[i+1] > x和A[j] <= x。
修复之后(也包括增加i),我们回到不变式为真。
嵌套循环示例
现在我们已经看到了一个基本的例子,现在是时候把我们的注意力转向迭代算法中另一个常见现象的问题,即嵌套循环集。在下一个例子中,我们将学习一种叫做冒泡排序的排序算法。这是一个相对低效的排序算法的例子,但它有足够的复杂性,值得我们花时间研究它。
在下面的讨论中,符号A[1..]i]≤A[i+1..]n]表示A[1..]范围内的每个元素。i]小于或等于A[i+1..n]范围内的赢博体育元素。”此外,如果两个范围中的一个或两个都为空,则该语句被理解为平凡的真。
的代码
假设一个[1 . .N]是一个初始未排序的整数数组。下面是一些使用冒泡排序算法对数组进行排序的代码。
I = 1;While (i <= n) {j = n;而(j >我){如果([j] < (j - 1)) {temp = (j - 1);A[j-1] = A[j] = A[j] = temp;} j——;}我+ +;}
内循环分析
由于这段代码的结构是一对嵌套循环,我们将依次对这两个循环赢博体育证明技术。由于外部循环将依赖于内部循环,因此我们从内部循环开始分析。
<初始化> = “j = n”
<终止> = “j = i”
这个不变量在初始化时通常为真,因为A[j+1..]N]为空。也很容易看出
在循环体的开始,我们知道A[j]是A[j…n]中最小的元素。如果A[j]也小于A[j-1],我们将两个位置交换,使A[j-1]≤A[j..n]。否则,我们保留A[j-1],使A[j-1]再次≤A[j..n]。在循环体末尾对j进行减量之后,不等式又变成了不变量,因为减量有效地将j-1替换为j。
外回路分析
<初始化> = “i = 1”
<终止> = “i = n + 1”
在初始化时,不变量通常为真,因为范围A[1..]I-1]为空。
<不变>
+
<终止>
=
<目标>
,因为在终止时间A[1..]i-1] = A[1..]n]和范围A[i…]N]终止时为空。这意味着在终止时不变量化为“(A[1..]N]被排序)和(true)”,这与
在外环体的开始,我们有“(A[1..i-1]排序)和(A[1..]i-1]≤A[i..n]]”。在执行了内部循环之后,我们还得到了“A[i]≤A[i+1..n]”。条件(A[1..]i-1]≤A[i..n])意味着A[i-1]≤A[i],因为A[i]只是更大范围A[i..]的一个元素。n]和A[i-1]代表范围A[1..i-1]。结合([1 . .(A[i-1]≤A[i])得到(A[1..]I]排序)。这保持了不变量的前半部分。耦合内环目标“A[i]≤A[i+1..”n " with (A) [1..]i-1]≤A[i..n])得到(A[1..]i]≤A[i+1..n]),保持不变式的后半部分。
内循环执行后,我们得到“(A[1..i]排序)和(A[1..]i]≤A[i+1..n]]”。在外部循环体末尾增加i,将不变量恢复为原始的“(A[1..]i-1]排序)和(A[1..]i-1]≤A[i..n]]”。
第21章算法的正确性证明
令人惊讶的是,我们在第21章学习的两种算法,Kruskal算法和Prim算法,都有相同的正确性证明。
证明包括首先将两个算法重写为等效的通用MST算法:
通用的MST
general - mst (G,w) A =∅当A不形成生成树时,找到一条对A安全的边(u,v) A = A′{(u,v)}返回A
该算法依赖于一些特殊的定义
- 切是将一个顶点集合细分为一个集合S和它的补集V-S。
- 如果一条边连接了S中的一个顶点和V-S中的一个顶点,那么它就穿过了切面。
- 如果A中的赢博体育边都不与切割相交,那么切割就符合集合A。
- 如果一个是MST的子集T和E这是一条边吗E是安全为一个如果一个∪{E}是MST的一个子集T
 .
.
首先,为什么Kruskal和Prim都是通用算法的例子?答案在于每个算法在每轮上构造集合S的独特方式。在Prim的算法中,A只是我们目前选择的边的集合,集合S总是我们通过使用A中的边来连接的顶点的集合。对于Kruskal,我们关注的是Kruskal想要使用的下一条边。如果这条边不与我们已经选择的边形成一个循环,它将与图的组成部分连接在一起。诀窍就是让S等于这两个分量中的一个注意我们要选的边是穿过S周围的切口的最便宜的边。
通用MST算法中while循环的正确性证明取决于以下定理:
定理21.1
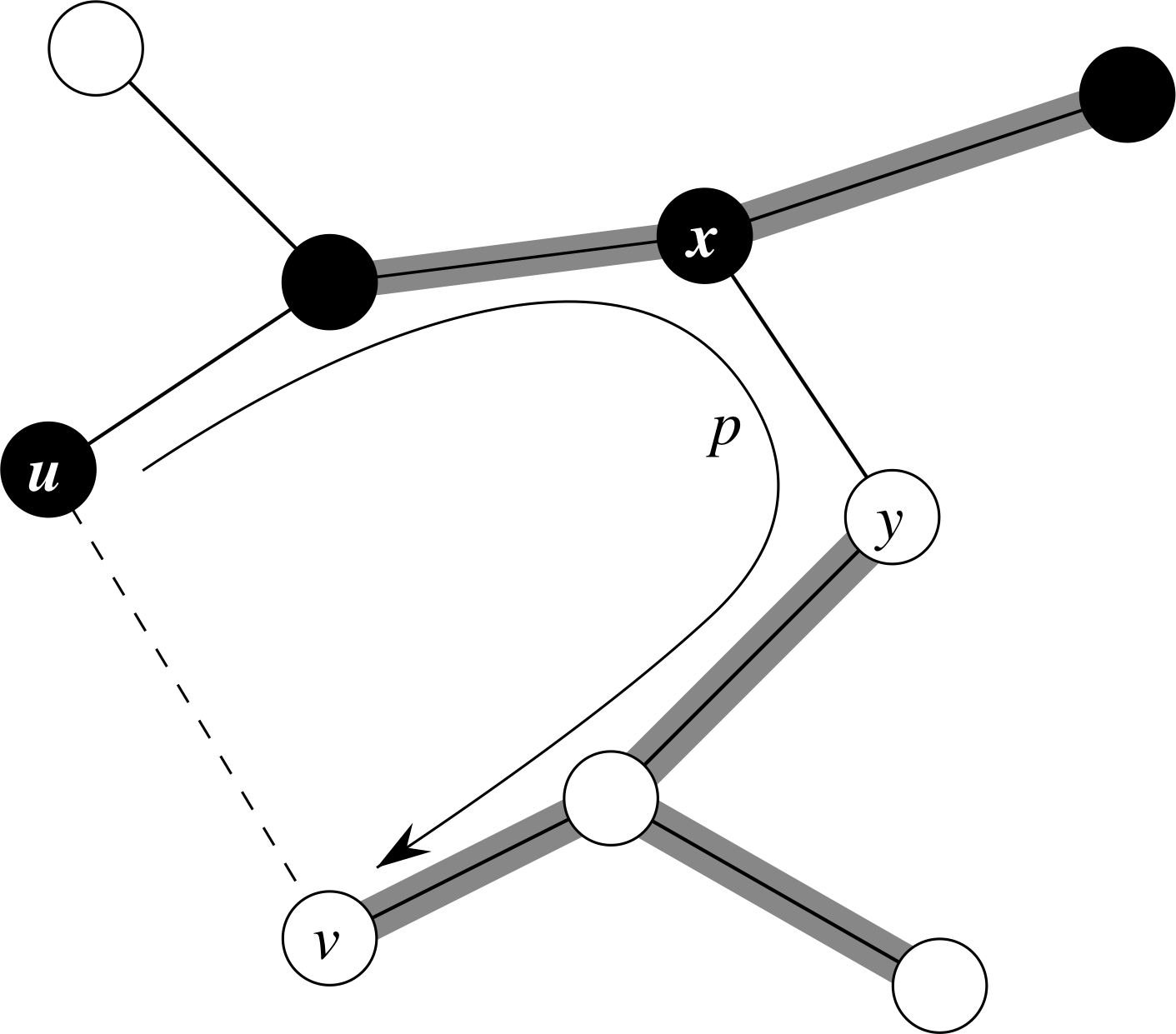
设G = (V,E)是一个连通的无向图,其实值权函数w定义在E上,设a是E的一个子集,它包含在G的某个最小生成树中,设(S,V-S)是G对a的任意切点,设(u, V)是一条穿过(S,V-S)的轻边。那么,边(u,v)对于A是安全的。
我要让你们参考课本来阅读这个定理的证明,它给出了如下的论证。
Dijkstra算法的正确性证明
这是Dijkstra算法的伪代码。
DIJKSTRA(G,w,s) INITIALIZE-SINGLE-SOURCE(G,s) s =∅Q = G.V而Q !=∅u = EXTRACT-MIN(Q) s = s′′{u}对于每个顶点v∈G. adj [u] RELAX(u,v,w)
Dijkstra算法的正确性证明依赖于以下循环不变量:
当u进入S(以及之后的赢博体育时间),u.d = δ(S,u)
再一次,我将引导你们去阅读原文来阅读证明的细节,它使用了一系列重要的引理:
子路径引理(21.1)如果s→→u→→v是s到v的最短路径,则s→→u是s到u的最短路径。
收敛引理(21.14)如果s→→u→v是s到v的最短路径,且在松弛边(u,v)之前任意时刻u.d = δ(s,u),则松弛边(u,v)之后任意时刻v.d = δ(s,v)。
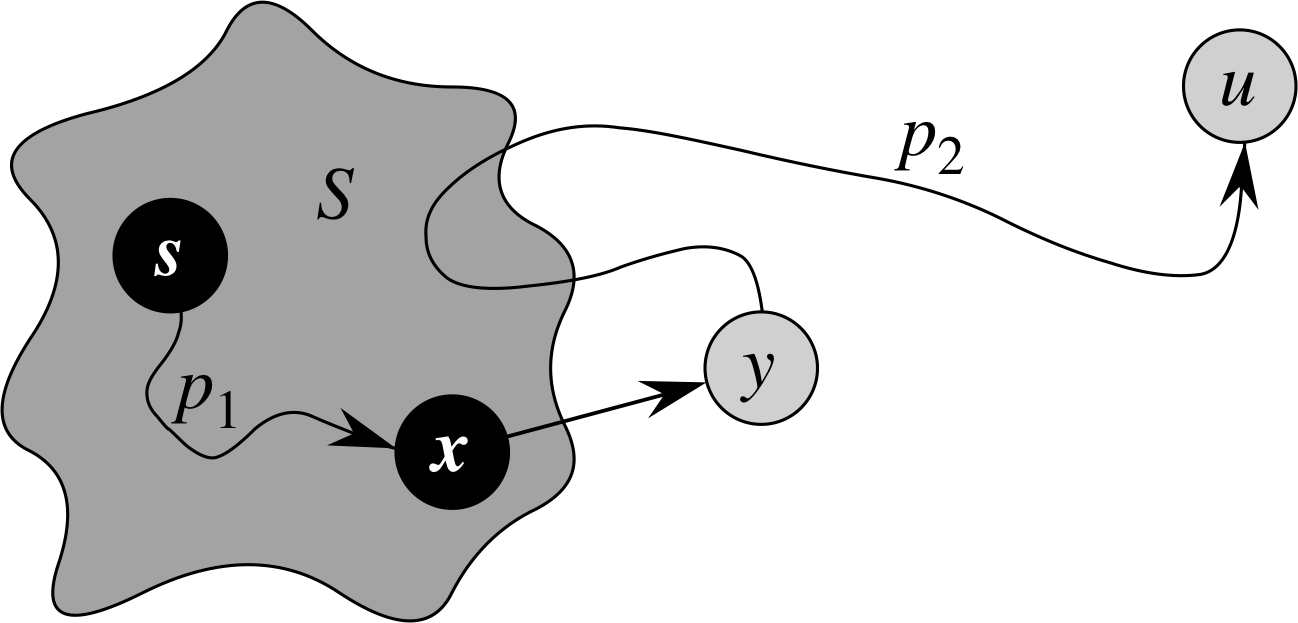
证明还依赖于一个关键步骤,如下图所示。
证明一个递归算法的正确性
我在这里介绍的技术为证明迭代算法是正确的提供了一个框架。递归算法需要一种不同的方法。幸运的是,有一种方法可以证明递归算法是正确的,这种方法在很多例子中都很有效:我们将归纳法赢博体育于递归。
为了说明它是如何工作的,让我们回顾一下快速排序。这里是该算法的完整伪代码:
QUICKSORT(A,p,r)如果p < r q = PARTITION(A,p,r) QUICKSORT(A,p,q-1) QUICKSORT(A,p,q-1) QUICKSORT(A,p,r) PARTITION(A,p,r) x = A[r] i = p-1 for j = p到r-1如果A[j] <= x i = i+1交换A[i]与A[j]交换A[i+1]与A[r]返回i+1
我在上面介绍的正确性证明技术允许我们声明,无论何时调用配分函数,它都会做正确的事情。为了将其推广到证明整个快速排序算法是正确的,我们构造了一个关于范围大小的归纳法证明。我们正在分类。
详情如下。
对于范围[p..]r],大小为0,我们将在快速排序算法中遇到基本情况。这个基本情况什么都不做,在对大小为0的数组进行排序时,这样做是正确的。
我们假设快速排序能够正确排序数组a [p..]R当范围的大小[p..]我们证明了快速排序可以对数组a [p..]的一部分进行排序。R当范围的大小[p..]r]等于n。以下是一些观察结果:
- 快速排序将首先在A[p..r]上运行分区算法。这将导致A[p.]r]被重组成A[p,q-1]部分,其中包含小于或等于A[q], A[p+1],…r]包含赢博体育大于A[q]的数字,以及A[q]本身。
- 然后我们递归地对A[p..][q+1]和[q+1..r]。由于这些子范围的大小都小于n,因此归纳假设允许我们假设这些子范围将被正确排序。
- 一旦子范围被排序,整个范围A[p..]R]是正确排序的。