多项式插值
多项式插值问题是构造一个多项式的问题,该多项式通过或插值n+1个数据点(x0, y0), (x1, y1),…, (xn, yn)。
拉格朗日插值
1795年,法国数学家约瑟夫·路易斯·拉格朗日(Joseph-Louis Lagrange)发表了一种从一组数据点构造插值多项式的算法。
构造一个n次多项式,通过n+1个数据点(x0, y0), (x1, y1),…, (xn, yn)我们首先构造一组基多项式Ln,k(x)它的性质是
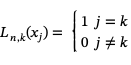
这些基多项式很容易构造。例如,对于一个x值序列{x0, x1, x2, x3},我们将有四个基多项式
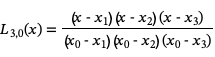
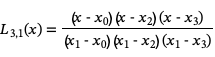
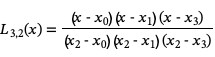
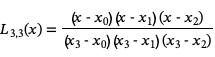
一旦我们构造了这些基函数,我们就可以形成第n次拉格朗日插值多项式
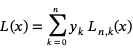
这个多项式做了我们想要的,因为当x = xj时赢博体育的基函数都消失了,除了Ln j(x)它的值是1。因此,对于每个j, L(xj) = yj,该多项式对原始数据集中的每一个数据点进行插值。
由于n次多项式是由它在n+1个点上的值唯一决定的,所以这是通过数据点的唯一多项式。
一个例子
这是一组数据点。
| x | y |
|---|---|
| 4.1168 | 0.213631 |
| 4.19236 | 0.214232 |
| 4.20967 | 0.21441 |
| 4.46908 | 0.218788 |
这是这些点的曲线图,显示它们沿着一条曲线排列,但这条曲线并不是完全线性的。
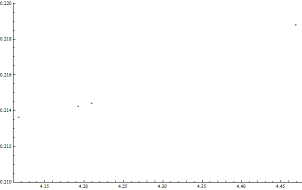 |
||||||||||
|
为了构造经过这些点的3次拉格朗日插值多项式,我们首先计算基函数:
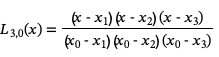
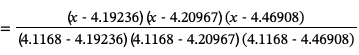
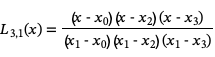
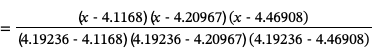
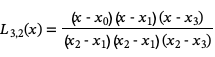
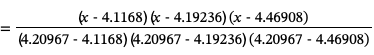
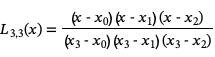
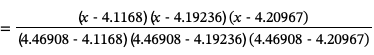
由此构造插值多项式:
L (x) = y0 L3, 0 (x) + y1 L3, 1 (x) + y2 L3, 2 (x) + y3 L3, 3 (x)
= -0.00355245 x3 + 0.0695519 x2 - 0.386008 x + 0.871839
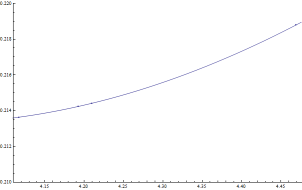
这里是原始数据点与插值多项式一起绘制。
 |
||||||||||
|
||||||||||
| y = -0.00355245 x3 + 0.0695519 x2 - 0.386008 x + 0.871839 |
计算拉格朗日多项式的程序
我们的下一个示例程序是一个从一组数据点构造和计算拉格朗日多项式的程序。我将利用这个程序来展示更多类的例子,并演示如何使用类将复杂的问题分解成更小更简单的部分。
一旦我们构建了一个程序,可以读取一组数据点,并从中构造一个插值多项式,我们将使用插值多项式来解决问题。
表示数据点的类
拉格朗日插值多项式由一组数据点构成,其中每个数据点是一个x值和一个y值的组合。
下面是一个简单类的代码,我们可以用它来表示我们的数据点。
包内插;公共类数据点{私有浮点x;Private float y;公共数据点(浮动x,浮动y){这。X = X;这一点。Y = Y;}公共浮点getX(){返回x;}公共浮动getY(){返回y;}}
表示数据集的类
数据点被组织成数据集。数据集就是数据点的列表。
下面是我构造的一个类来帮助我们对数据集建模:
包内插;进口java.util.ArrayList;进口并不知道;进口java.util.Scanner;公共类PointSet{私有列表<数据点>点;public PointSet() {points = new ArrayList<DataPoint>();}公共无效readFrom(扫描器输入){while(input. hasnextfloat ()) {float x = input. nextfloat ();float y = input.nextFloat();点。添加(新数据(x, y));}} public List<Float> getXs() {ArrayList<Float> result = new ArrayList<Float>();for(DataPoint dp: points) {result.add(dp. getx ());}返回结果;} public List<Float> getYs() {ArrayList<Float> result = new ArrayList<Float>();for(DataPoint dp: points) {result.add(dp. gety ());}返回结果;}}
由于我们将从文本文件中读取数据集,因此我在这里提供了一个成员函数来从文本文件中读取这些数据点。
我前面展示的拉格朗日插值算法大量使用了x值列表和y值列表。为了帮助我们从数据集生成这些列表,我还提供了getXs()和getYs()方法,它们分别返回x值列表和y值列表。
一个表示拉格朗日多项式的类
下一个我们要学习的类是一个代表拉格朗日多项式的类它是我们从一组数据点构造出来的。下面是该类的代码。
包内插;进口java.util.ArrayList;进口并不知道;公共类LagrangePoly{私有列表<Float> ys;private List<BasisFunction> ls;public LagrangePoly(PointSet data) {ys = data. getys ();List<Float> xs = data.getXs();ls = new ArrayList< basefunction >();For (int k = 0;k < xs.size();k++) {1;添加(新BasisFunction (xs, k));}}公共float evalAt(float x) {float sum = 0.0f;(int k = 0; k < ys.size (); k + +){总和+ = ys.get (k) * ls.get (k) .evalAt (x);}返回sum;}}
注意,该类的构造函数接受一个PointSet对象作为参数。从这组数据点中,类将构造基函数列表和组成多项式的y值。
由于我们正在构造一个多项式,我们最终会想要在某个x值处计算这个多项式的值。为了实现这一点,我提供了一个evalAt()方法,它在给定的x值处计算多项式,并返回该x处的多项式值。
需要解决的问题
在我提供的项目中,您还可以找到一个名为population.txt的文本文件。该文本文件包含1960年至2010年美国人口普查的人口数据。我们将从这些数据中构造一个插值多项式,并用它来估计1985年的美国人口。
我还为您提供了最后一个类,其中包含您将用于解决此问题的主要方法:
包内插;进口java.io.File;进口java.util.Scanner;public class Interpolation {public static void main(String[] args) {Scanner输入;try {input = new Scanner(new File("population.txt"));} catch(Exception ex) {ex. printstacktrace ();返回;} PointSet points = new PointSet();points.readFrom(输入);input.close ();LagrangePoly = new LagrangePoly(点);input = new Scanner(System.in);system . out。print(“输入年份:”);int year = input.next ();system . out。println(“+ year +”中美国的近似人口为“+ (int) p.evalAt(year));}}
缺失的课程
我故意在我的程序中遗漏了一个类。您的工作将是为缺少的BasisFunction类编写代码。从我提供的代码中,您可以看到该类的构造函数将采用什么形式,并且您还可以看到该类需要有一个evalAt()方法,该方法允许您根据给定的x值计算基函数。
这里有一个有用的提示:从上面的讨论中你可以看到,基函数是一个分数,它的分子取决于x值和数据点的x值,分母只取决于数据点的x值。这意味着您可以提前计算出分母并将其存储在成员变量中。这样,evalAt()方法只需要计算分子,然后除以预先计算的分母。